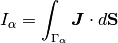Physical models¶
Concentrations of charges in thermal equilibrium¶
Probability 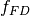 that an electronic state with energy
that an electronic state with energy 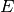 is occupied is given by the Fermi-Dirac distribution:
is occupied is given by the Fermi-Dirac distribution:
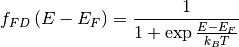
with 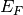 denoting the Fermi energy,
denoting the Fermi energy, 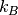 denoting the Boltzmann constant and
denoting the Boltzmann constant and 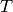 denoting the temperature.
denoting the temperature.
The states in the conduction band are distributed in energy according to the density of states function 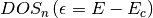 . The total concentration
. The total concentration 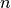 of electrons is given by integral
of electrons is given by integral
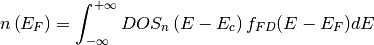
In the valence band, almost all states are occupied by the electrons. It is therefore useful to track unoccupied states, holes, instead of the occupied states. The concentration of holes is given by:
![p \left( E_F \right) = \int_{-\infty}^{+\infty} DOS_p \left( E_v - E \right) \left[ 1 - f_{FD}(E - E_F) \right] dE](_images/math/e0fc77cab24bfd0b463c8bf2d557693c187fc048.png)
Noting that
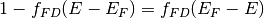
and changing the integration variable, both concentrations can be written in a common form as:
(1)¶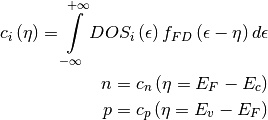
Practical note: The SI base unit of energy is Joule (J), however the energies such as 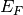 are very small and should be expressed in electronvolts (eV). The SI basic unit of concentration is
are very small and should be expressed in electronvolts (eV). The SI basic unit of concentration is 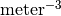 , although
, although 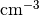 is often encountered. The value of
is often encountered. The value of 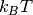 at the room temperature is approximately 26 meV. The SI unit of temperature is Kelvin,
at the room temperature is approximately 26 meV. The SI unit of temperature is Kelvin, 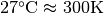 .
.
Band energies¶
In an idealized case, the energies 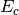 and
and 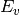 of the conduction and valence bands are
of the conduction and valence bands are
(2)¶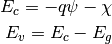
where 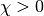 is the electron affinity energy, and
is the electron affinity energy, and 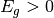 is the bandgap energy.
is the bandgap energy. 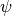 is the electrostatic potential. q is the elementary charge.
is the electrostatic potential. q is the elementary charge.
Electrostatic potential¶
The electric field 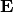 is related to the elestrostatic potential
is related to the elestrostatic potential 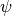 as
as
(3)¶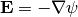
In linear, isotropic, homogeneous medium the electric displacement field is
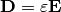
with permittivity
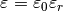
where 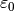 is the vacuum permittivity, and
is the vacuum permittivity, and 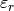 is the relative permittivity of the material.
is the relative permittivity of the material.
The electric displacement field satisfies the electric the Gauss’s equation
(4)¶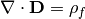
where 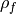 is the density of free charge
is the density of free charge
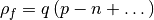
with 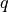 denoting the elementary charge. Above,
denoting the elementary charge. Above,  denotes other charges, such as ionized dopants.
denotes other charges, such as ionized dopants.
Combining the above equations gives the usual Poisson’s equation for electrostatics:
(5)¶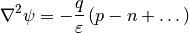
The SI unit of electrostatic potential is Volt, and the unit of electric field is Volt/meter. The unit of permittivity is Farad/meter. The unit of charge density is 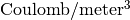 .
.
Approximation for low concentrations¶
If the concentration of charge carriers is low enough, only states on the edge of band gap are important. In such case, the density of states can be assumed as a sharp energetic level,
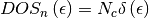
in case of electrons and
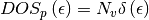
in case of holes. Substiting into (1) gives
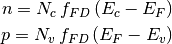
At low charge carrier concentrations, Fermi-Dirac distribution 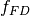 is simplified as
is simplified as
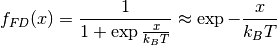
The approximation is considered valid when 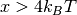 .
.
Approximate charge carrier concentrations are
(6)¶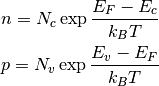
Gaussian density of states¶
In the case of Gaussian DOS, the density of states shape function 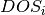 is the Gaussian distribution function scaled by total density of states
is the Gaussian distribution function scaled by total density of states 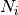 :
:
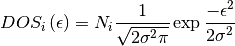
Concentrations of species are given by integral
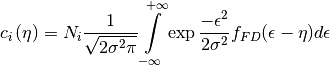
Conservation equation¶
The conservation equation is:

where 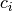 denotes the concentration,
denotes the concentration, 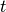 is time, and
is time, and 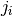 is the flux density.
is the flux density. 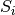 denotes source term, which is positive for generating particles, and negative for sinking particles of type i. The SI unit of source term is
denotes source term, which is positive for generating particles, and negative for sinking particles of type i. The SI unit of source term is 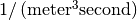 .
.
The conservation equation must be satisfied for each species separately. In the case of transport of electrons and holes, this gives
(7)¶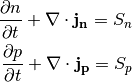
where the source S term contains for example generation 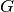 and recombination
and recombination 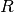 terms
terms
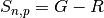
The conservation of electric charge must be satisfied everywhere. Therefore, the source terms acting at given point must not create a net electric charge. In the case of system of electron and holes, this requires
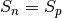
Current density¶
Current density 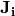 is related to the density flux
is related to the density flux 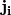 by the charge of single particle
by the charge of single particle 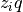 . Obviously, for electrons
. Obviously, for electrons 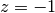 and for holes
and for holes 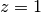 , therefore
, therefore
(8)¶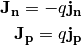
Note that a convention is adopted to denote the electric current with uppercase letter 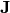 , and the flux density with lowercase letter
, and the flux density with lowercase letter 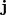 . The SI unit of density flux
. The SI unit of density flux 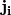 is
is 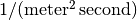 , while the unit of electric current density
, while the unit of electric current density 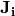 is
is 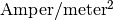 .
.
Equilibrium conditions¶
In the equilibrium conditions, Fermi level energy 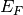 has the same value everywhere. The electrostatic potential
has the same value everywhere. The electrostatic potential 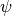 can vary, and the density of free charge
can vary, and the density of free charge 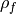 does not need to be zero. Equations (1), (2), (4) are satisfied simultaneously. The current flux, the source terms, and the time dependence are all zeros, so conservation (7) is trivially satisfied.
does not need to be zero. Equations (1), (2), (4) are satisfied simultaneously. The current flux, the source terms, and the time dependence are all zeros, so conservation (7) is trivially satisfied.
Nonequilibrium conditions¶
In the non-equilibrium conditions, the transport is introduced as a perturbation from equilibrium. The Fermi energy level is replaced with quasi Fermi level, which is different for each species. In (1), the equilibrium Fermi level for electrons 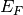 is replaced with a quasi Fermi level
is replaced with a quasi Fermi level 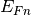 . Similarly,, the equilibrium Fermi level for holes is replaced wuth quasi Fermi level for holes
. Similarly,, the equilibrium Fermi level for holes is replaced wuth quasi Fermi level for holes 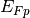 , giving
, giving
(9)¶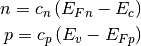
Quasi Fermi levels have associated quasi Fermi potential according to the formula for energy of an electron in electrostatic field 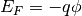 :
:
(10)¶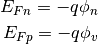
The transport is modeled by approximating electric current density as
(11)¶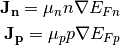
where 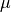 denotes the respective mobilities. The SI unit of mobility is
denotes the respective mobilities. The SI unit of mobility is 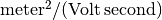 , although
, although 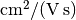 is often used.
is often used.
Equations (2), (5), (9), (11), (7) are simultaneously satisfied in non-equilibrium conditions.
Drift-diffusion system¶
Standard form of density fluxes in the drift-diffusion system is
(12)¶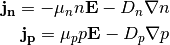
or more generally, allowing arbitrary charge 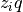 per particle
per particle
(13)¶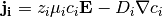
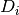 is the diffusion coefficient, with SI unit
is the diffusion coefficient, with SI unit 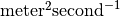 .
.
Drift-diffusion system: low concentration limit¶
To obtain the conventional drift-diffusion formulation (12), the the low concentration approximation (6) should be used. After introducing quasi Fermi levels, as it is done in (9), one obtains
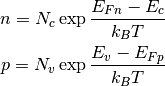
From that, the quasi Fermi energies are calculated as
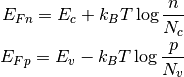
Using (2), and assuming constant ionization potential 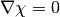 , bandgap
, bandgap 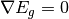 , constant total densities of states
, constant total densities of states 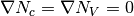 , and constant temperature
, and constant temperature 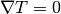 , substituting into (11), and using (3)
, substituting into (11), and using (3)
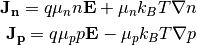
In terms of density flux (8), this reads
(14)¶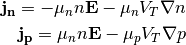
where thermal voltage
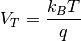
Einstein’s relation¶
Equation (14) is written in the standard drift-diffusion form (12) when the diffusion coefficient satisfies
(15)¶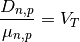
This is called Einstein’s relation.
Drift-diffusion system: general case¶
Using functions defined in (1), bands (2) and approximation (9)
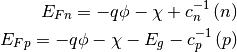
current densities under assumptions 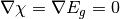 are
are
(16)¶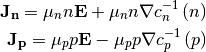
Generalized Einstein’s relation¶
In equation (16), assuming 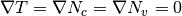
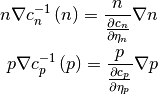
In order to express equation (16) in the standard drift-diffusion form (12), the diffusion coefficient must satisfy
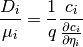
This is so called generalized Einstein’s relation .
Intrinsic concentrations¶
Intrinsic concentrations 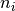 ,
, 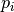 , and intrinsic Fermi level
, and intrinsic Fermi level 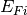 satisfy electric neutrality conditions
satisfy electric neutrality conditions
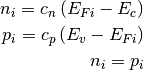
Unidimensional form¶
By substituting 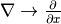 and
and 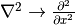 , the equations (5), (7), (12) of the basic drift-diffusion device model are
, the equations (5), (7), (12) of the basic drift-diffusion device model are
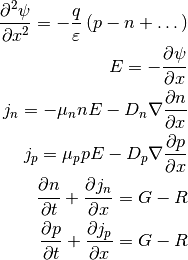
Total electric current density¶
Total electric current 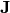 is a sum of currents due to transport of each species and the displacement current
is a sum of currents due to transport of each species and the displacement current 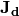
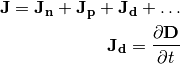
Total electric current satisfies the conservation law
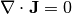
This can be verified by taking time derivative (4), using (7) and considering that the sum of all charge created by the source terms must be zero.
Metal¶
In metal, the relation between the electrostatic potential  , the workfunction energy
, the workfunction energy  and the Fermi level
and the Fermi level 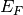 is
is
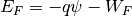
On the other hand, the Fermi potential corresponds to the applied voltage 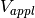
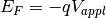
This leads to electrostatic potential at metal surface
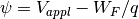
Ohmic contact¶
Ohmic contact is an idealization assuming that there is no charge accumulation at the contact, and the applied voltage 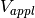 is equal to quasi Fermi potentials (10) of charged species
is equal to quasi Fermi potentials (10) of charged species
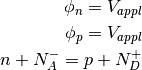
Above three conditions uniquely determine the charge concentrations 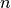 ,
, 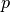 , and the electrostatic potential
, and the electrostatic potential 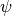 at the contact.
at the contact.
Electrochemical transport¶
Electrochemical potential for ionic species is
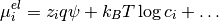
It should be noticed that so defined “potential” has the unit of energy, unlike the electrostatic potential and quasi Fermi potentials. Above  denote corrections, for example due to steric interactions. Electrochemical potential
denote corrections, for example due to steric interactions. Electrochemical potential 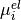 should not be confused with mobility
should not be confused with mobility 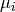 .
.
Density flux is approximated as
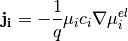
yielding the standard form (13) using Einstein’s relation (15).
Electrochemical species should be included in Poisson’s equation, by including proper source terms of form 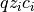 . A variant of Poisson’s equation (5) where are free charges are ions can be written as
. A variant of Poisson’s equation (5) where are free charges are ions can be written as
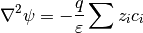
Steric corrections¶
To account for finite size of ions, the electrochemical potential in the form introduced in [LE13] is useful
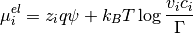
where 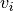 denotes volume of particle of type
denotes volume of particle of type 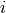 .
. 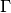 is the unoccupied fraction of space
is the unoccupied fraction of space
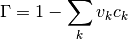
where summing is taken over all species occupying space, including solvent.
| [LE13] | Jinn-Liang Liu and Bob Eisenberg. Correlated Ions in a Calcium Channel Model: A Poisson–Fermi Theory. The Journal of Physical Chemistry B, 117(40):12051–12058, 2013. PMID: 24024558. URL: https://doi.org/10.1021/jp408330f, arXiv:https://doi.org/10.1021/jp408330f, doi:10.1021/jp408330f. |
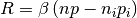
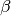 can be chosen freely.
can be chosen freely.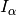 passing through a surface
passing through a surface 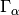 of electrode
of electrode 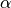 is
is